برای تشخیص اینکه یک عدد ، اول است یا نه، می‌توانیم آن را بر تمام اعداد کوچکتر از خودش تقسیم کنیم. اگر فقط بر 1 و خودش بخش‌پذیر بود،   اول است.

حتی بهتر ، می تونیم بر تمام اعداد اول  کوچک تر از جذر عدد تقسیم کنیم و اگر بر هیچ کدام بخش پذیر نبود اول است . (به نظرت چرا این کار هم جواب میده ؟ می تونی تو کامنت برام بنویسی ) 

مثال :

• آیا عدد 143 اول است ؟

کافیست بررسی کنیم عدد 143 بر اعداد کوچکتر از خودش بخش پذیر است یا نه ، حالا چون این اعداد زیادن ، گفتیم می تونیم چک کنیم عدد 143 بر اعداد اول کوچک تر از جذرش بخش پذیر است یا نه ؟

جذر 141 : (تقریبا) 11.9

اعداد اول کوچک تر از 11.8 ==> 2 و 3 و 5 و 7 و 11

•  بر 2 و 5 بخشپذیر نیست (چون رقم یگانش نه زوجه نه 0 یا 5 )
• بر 3 بخشپذیر نیست ، چون مجموع ارقامش بر 3 بخشپذیر نیست
•  بر 7 و 11 بخشپذیر نیست ، چون وقتی تقسیم کنیم باقی مونده داره

پس عدد 141 عدد اول است .

• سوال:

• آیا عدد 29   اول است؟

• بخشپذیری عدد 103 را حداقل بر چند عدد باید چک کنیم تا تشخیص بدیم اوله یا نه ؟

اعداد اول در بسیاری از جنبه‌های زندگی و علم کاربرد دارند. در ریاضیات، آنها پایه‌ی ساختار عددی هستند ، برای درک بهتر می تونی از ویدئو ی این لینک استفاده کنی ،

در ادامه به برخی از مهم‌ترین کاربردهای آن‌ها اشاره می‌کنم:

• نظریه اعداد و ریاضیات محض (مثلا تابع اویلر و …)
• علوم کامپیوتر ( در فشرده سازی داده ها ، الگوریتم های تصادفی و … )
• فیزیک
• فیزیک ذرات: اعداد اول در برخی مدل‌های فیزیک ذرات برای توصیف خواص ذرات بنیادی استفاده می‌شوند.
• کریستالوگرافی: اعداد اول در تحلیل ساختار کریستالی برخی مواد کاربرد دارند.

و … کاربرد دارند

یکی از مهم‌ترین کاربردهای این اعداد  در علوم کامپیوتر و به خصوص در رمزنگاری است.

اعداد اول به دلایل مختلفی بسیار مهم هستند. یکی از این دلایل این است که هر عددی را می‌توان به عنوان حاصل‌ضرب اعداد اول نوشت. این فرآیند تجزیه اعداد به عوامل اول نامیده می‌شود.

مثلاً عدد ۱۲ را می‌توان به صورت ۲ × ۲ × ۳ نوشت.

این کار به ما کمک می‌کند تا ساختار اعداد را بهتر درک کنیم و روابط بین اعداد را بهتر بفهمیم.

حالا یک ویژگی خیلی مهم این اعداد اینه که اگر ما دو تا عدد اول بزرگ داشته باشیم ، راحت می تونیم در هم ضرب کنیم و حاصل ضربشونو به دست بیاریم ،

ولی اگر حاصل ضربشونو به ما بدن ، تجزیه ی حاصل ضرب به عوامل اول سازنده اش کار سختیه .

مثلا اگر ما 29 و 23 را داشته باشیم ، راحت می تونیم در هم ضربشون کنیم و حاصل که میشه 667 را حساب کنیم

اما اگر به ما بگن دو تا عدد اولی که حاصل ضربشان عدد 667 را می سازد ،باید با آزمون و خطا پیداشون کنیم

یعنی بر اعداد اول کوچک تر از جذرش (که تقریبا 25 و خورده ای عه ) تقسیم کنیم تا ببینیم بر کدوم عدد اول بخش پذیره و اجزای سازنده اش را پیدا کنیم ، یعنی باید 9 تا(چون تعداد اعداد اول کوچک تر از 25 ،9 تاست ) تقسیم انجام بدیم

خب این کار خیلی زمان بره دیگه . حالا تازه اینجا اعداد  خیلی بزرگی رو انتخاب نکردیم ، فکر کن اگر عدد 1887 رو بهمون بدن و بگن این عدد از حاصل ضرب دو عدد اوله ، اون دو تا رو پیدا کن چقدر باید محاسبه کنیم ، یا حتی اعداد بزرگتر

راستش اصلا یه فرضی تو ریاضیات هست که می گه برای اعداد خیلی خیلی بزرگ ، پیدا کردن دو عدد اولی که اون عدد رو ساختن کاره خیلی خیلی سختیه ، اونقدر سخت که برای رمزگذاری ها از این ویژگی اعداد اول استفاده میشه ، این که چطوری استفاده میشه یه ذره زوده ولی اگر خواستی درباره ی این کاربرد بیشتر بدونی ، در باکس پایین صفحه بهم بگو .

اعداد اول و ارتباط آن‌ها با اعداد غیر اول
از اونجایی که همه ی اعداد ، از حاصل ضرب یک یا چند عدد اول مختلف به دست می آید و به بیانی اعداد اول خالق تمام اعداد طبیعی دیگر اند ، برای پیدا کردن کوچکترین مضرب مشترک دو عدد هم ، از عوامل اول آن‌ها استفاده می‌کنیم.

برای مثال ، برای به دست آوردن کوچکترین مضرب مشترک دو عدد ۴ و ۶ ، کافیه دو تا عدد رو به عوامل اولشون تجزیه کنیم

4 = 2× 2

6= 2 × 3

[ 4, 6 ] = 2× 2 × 3

یعنی تمام عوامل سازنده ی هر عدد ،تقسیم بر عامل مشترک سازنده اشون .که اینجا عدد 2، عامل مشترک سازنده ی 4 و 6 عه

حالا اگر دو عدد عامل مشترک نداشتن ، ک . م . م آن ها بزرگ تر بود و درواقع ک . م . م آن ها می شد حاصل ضرب دو عدد

پس بزرگترین مقداری که  ک . م . م هر دو عدد می تونه داشته باشه ، حاصل ضربشونه

کاربردهای جالب اعداد اول در دنیای واقعی

حالا فرض کن یه جیر جیرک داریم که سالی a بار از زیر زمین میاد بیرون

شکارچی این جیرجیرک هم سالی b بار روی زمینه

حالا قبول داری اولین باری که این دو تا در مقابل هم قرار می گیرند ، همون ک . م . م دو تا عدد a و b  عه

خب به نظرت a و b  چه جوری باشن که احتمال زنده موندن جیر جیرکه  بنده خدا بیشتر بشه و با شکارچیش روبرو نشه

آفرین اول از همه عامل مشترک نداشته باشن و بعد هم تا جایی که میشه اعداد بزرگی باشن که حاصل ضربشون بزرگ بشه تا ک . م . م آن ها هم بزرگ بشه و دیر تر مقابل هم قرار بگیرند

اتفاقا جیرجیرک باهوش هم اعداد اول رو خوب شناخته و هر 13 تا 17 سال یه بار میاد بیرون از زمین ، چون میدونه شکارچیش هر 2 سال یه بارمیاد بیرون  و با خوش گفته من اگر هر 13 سال یه بار بیام بیرون 26 سال دیگه قراره شکارچی مو ببینم .

حتی اگر شکارچی هم سال هایی که میاد بیرون و تغییر بده و مثلا 5 سال یه بار بیاد بیرون ، باز به نفع جیر جیرک میشه ،  چون هر چه  b ، بزرگتر باشه ، حاصل ضرب دو عدد بزرگتر میشه و چون a اوله و نسبتا بزرگ هم هست ، حالا حالا ها طول میکشه تا a و  b  عامل مشترک پیدا کنند ، پس ک . م . م میشه همون حاصل ضرب دو عدد که بزرگ تر میشه

پس جیرجیرک از یه عدد اول بزرگ برای کمک به بقای خودش استفاده کرد

با وجود این‌که اعداد اول ساده به نظر می‌رسند، هنوز هم بسیاری از رازها و سوالات حل‌نشده در مورد آن‌ها وجود دارد. مثلاً:

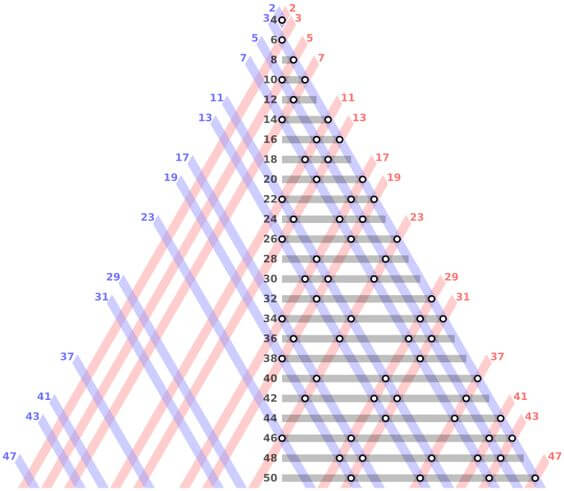
آیا می‌توان فرمول دقیقی پیدا کرد که تمام اعداد اول را تولید کند؟ 

آیا بی‌نهایت دوقلوهای اول (دو عدد اول که فقط یک واحد با هم فاصله دارند) وجود دارند؟

این سوالات هنوز پاسخ مشخصی ندارند و این یکی از دلایلی است که این اعداد همچنان برای ریاضی‌دانان جذاب و هیجان‌انگیز هستند.